Как сделать платформу Стюарта на Arduino

Привет, друзья!

Надоело делать обычных колёсных роботов? У нас есть идея поинтереснее: робот-гексапод с платформой Стюарта на шести сервоприводах.

Хотите разобраться, какова кинематика этого чуда и как это всё работает? Тогда садитесь поудобнее и изучайте вместе с нами!

Обратите внимание: платформа Стюарта — достаточно сложный проект, который потребует от вас определённых инженерных навыков и опыта в программировании на C++. Если вы сомневаетесь, что вам это подходит, повторите проект попроще, например робота для езды по линии.

Содержание

• Что такое платформа Стюарта
• Математическое описание платформы Стюарта
• Симуляция платформы Стюарта
• Дизайн и конструирование платформы
• Управление платформой
• Платформа-балансир
• Платформа-балансир на Raspberry Pi
• Заключение

Что такое платформа Стюарта

Платформа Гофа — Стюарта — это разновидность параллельного манипулятора, где используются шесть линейных приводов, скомпонованных по октаэдральной форме. Из-за такой шестиногой конфигурации этот манипулятор ещё иногда называют «Гексаподом» (Hexapod).

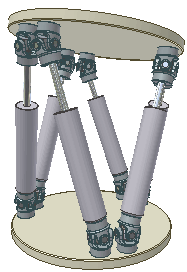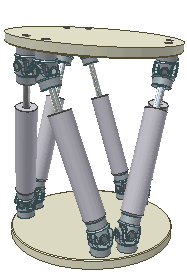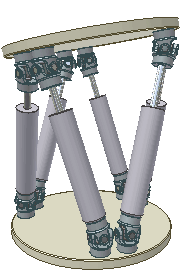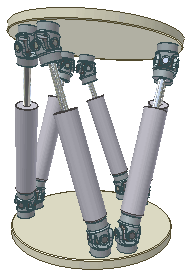
В общем виде манипулятор состоит из двух платформ. Первая платформа — нижняя, опорная или базовая (Base), она жестко зафиксирована на земле. Вторая платформа — верхняя, подвижная и управляемая. Верхняя платформа соединена с нижней платформой шестью ногами (Legs) в виде линейных приводов. Шесть ног попарно прикреплены к трём точками на нижней платформе и к трём точкам на верхней платформе. Ноги крепятся к платформам через универсальные шарниры. Суммарно получается 12 шарниров — шесть сверху и шесть снизу. Линейные приводы могут изменять длину ног и тем самым изменять ориентацию верхней платформы.

Верхняя платформа манипулятора имеет 6 степеней свободы (6-DoF). То есть верхняя платформа может не только двигаться по трём осям декартовой системы координат — вперёд/назад, вверх/вниз, влево/вправо, но и вращаться вокруг этих осей. Физически верхняя платформа может принимать любой внешний вид в соответствии с необходимым конечным эффектором кинематической цепочки (End effector).

Задача прямой кинематики, когда для заданных длин ног необходимо найти положение и ориентацию верхней платформы, может иметь до 40 решений. Однако задача обратной кинематики, когда по заданному положению и ориентации верхней платформы требуется найти длины ног, имеет единственное решение. Этот факт делает платформу Стюарта простой в освоении и управлении.

Тип используемых в ногах платформы Стюарта приводов зависит от конкретной области применения манипулятора и технических требований. Чаще всего используются линейные гидравлические приводы, реже пневматические, ещё реже электрические. В частных случаях в ногах используют не линейные, а поворотные приводы. Это решение усложняет кинематическую цепочку манипулятора, но может сделать его дешевле.

Несмотря на стоимость и сложность конструкции, платформы Стюарта очень распространены по всему миру. Вот несколько примеров использования.

Полётные тренажёры самолёта Airbus A380:

Радиотелескоп AMiBA:

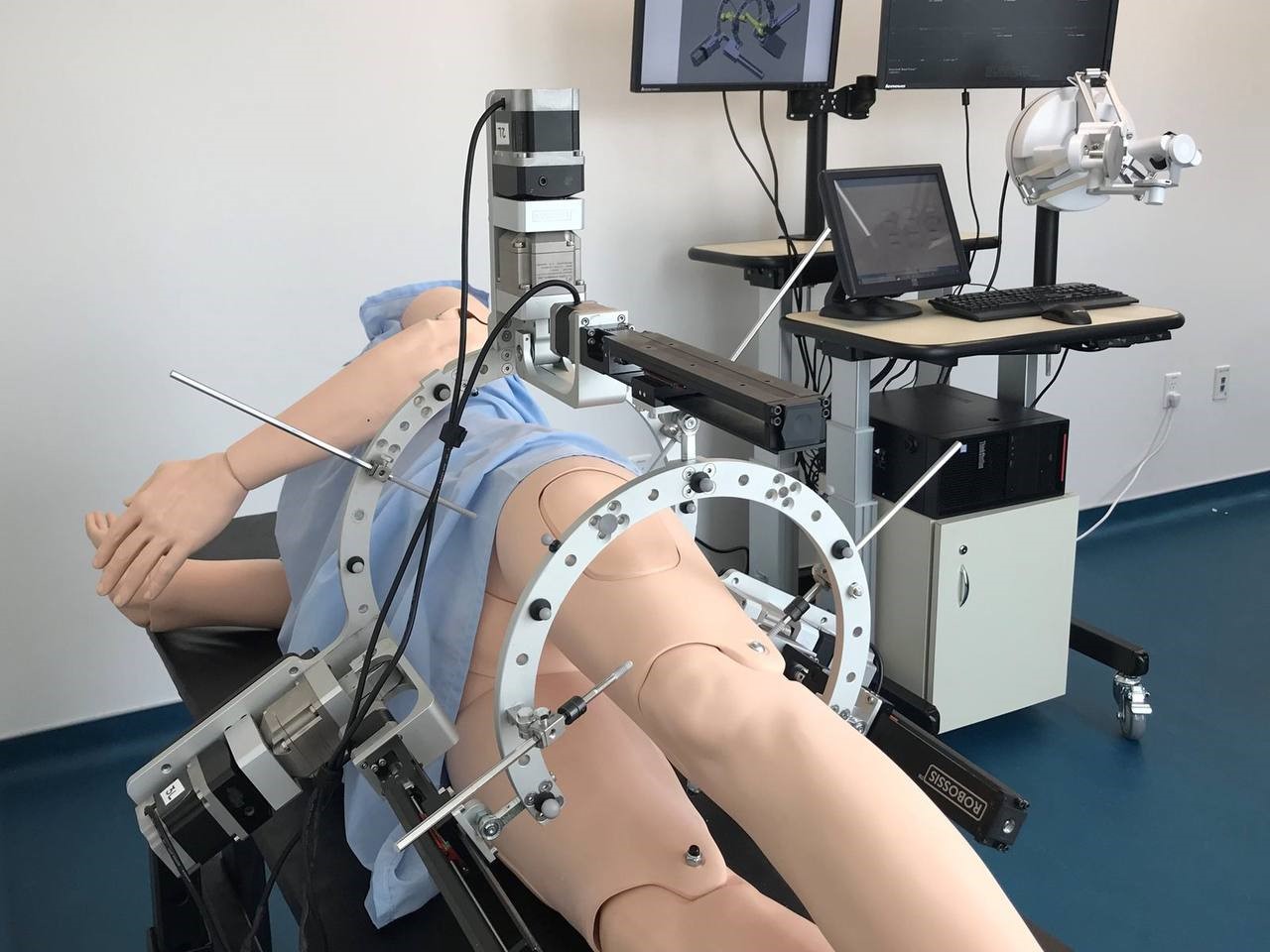
Трёхприводная платформа Стюарта применяется в медицине для репозиции сломанных костей:

Платформа Стюарта используется для стыковки космических аппаратов:

Гексапод Fanuc F-200iB на производстве:

Математическое описание платформы Стюарта

Чтобы создать программу для управления платформой Стюарта, нам нужно разобраться, как она устроена математически.

Приведённое ниже математическое описание — вольный перевод статьи неизвестного автора из математической группы Wokingham u3a.

В данном проекте будем использовать частный случай платформы Стюарта, построенной на поворотных приводах, а не линейных. Это связано с тем, что линейные приводы редко используются в хобби-робототехнике и электронике, а также отличаются дороговизной. Мы хотим сделать доступный для повторения проект, в то время как даже самые маленькие электрические линейные приводы, представленные на рынке, нельзя назвать дешёвыми. Поворотные приводы добавляют в кинематическую модель платформы Стюарта дополнительные расчёты, но мы начнём разбор именно с классической модели с линейными приводами.

Итак, платформа Стюарта состоит из двух жёстких платформ, соединённых между собой шестью ногами (Legs) переменной длинны. Нижнюю платформу будем называть базовой или базой (Base), а верхнюю — просто платформой (Platform). Так как точки крепления ног (для конкретной платформы) расположены на одинаковых расстояниях, мы можем условно представить платформы в виде двух окружностей или дисков. Точки крепления ног к базе и платформе представляют собой универсальные шарниры.

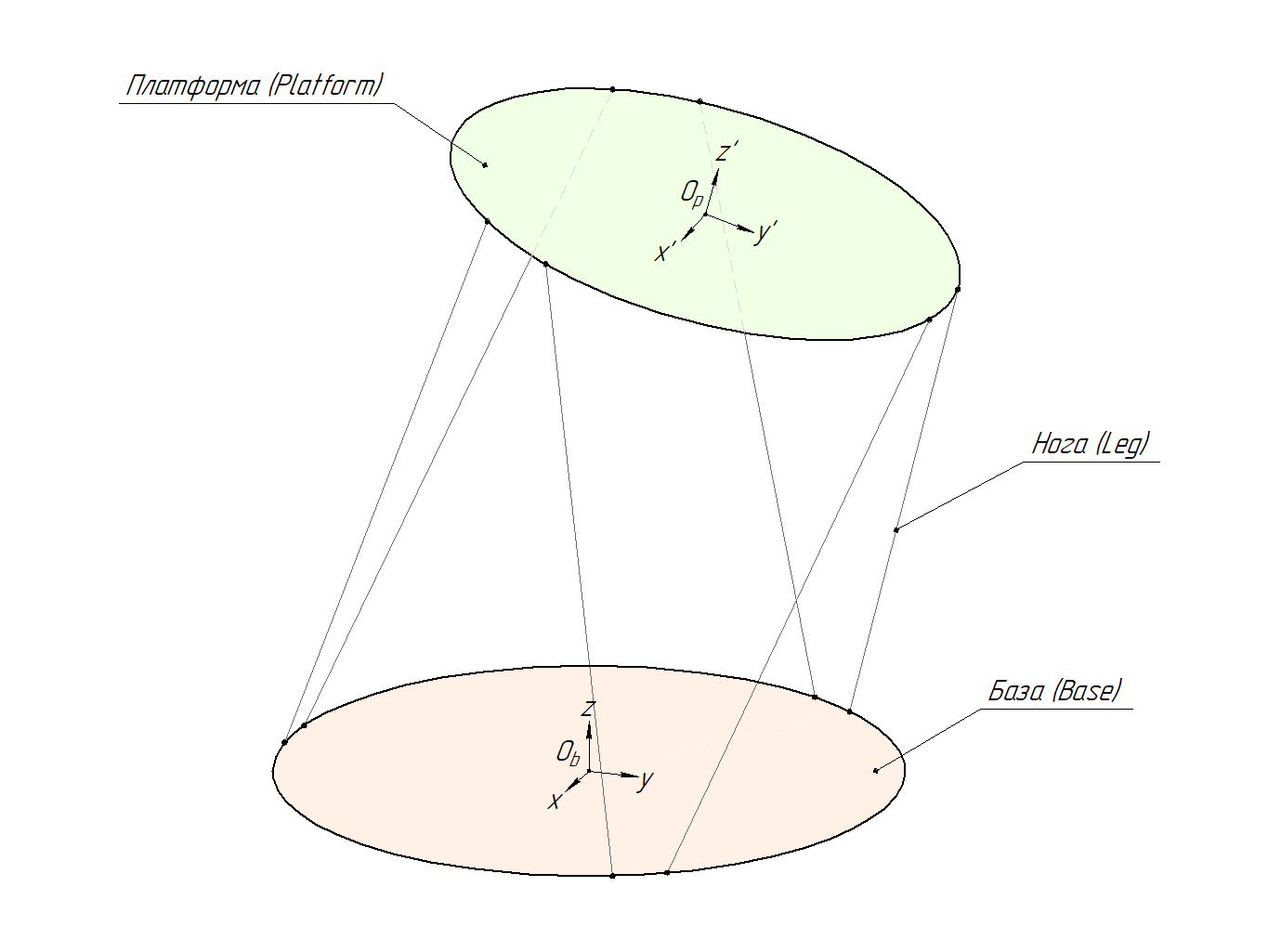
И база, и платформа имеют собственные прямоугольные системы координат. Пусть база имеет систему координат O_b(x, y, z), а платформа систему координат O_p(x’, y’, z’).

Суть задачи — узнать длину ног, зная точное расположение и ориентацию платформы относительно базы.

Расположение платформы, то есть начало координат O_p, определяется с помощью 3 поступательных линейных перемещений (Translation) относительно O_b вдоль осей х, у, z основания.

Ориентацию платформы (Rotation) по отношению к основанию можно определить тремя углами Эйлера. Угол ψ (пси) определяет поворот вокруг оси z, угол θ (тета) — поворот вокруг оси y, а угол φ (фи) — поворот вокруг оси x.

Для расчёта вращения платформы относительно базы воспользуемся матрицами поворота. Например, при повороте платформы относительно оси z базы на угол ψ матрица поворота R_z(ψ) имеет вид:

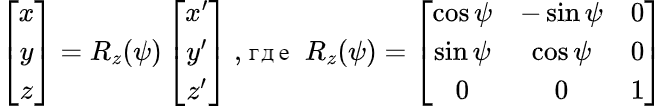
При повороте вокруг оси y на угол θ:

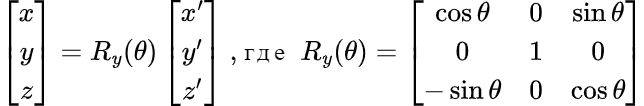
При повороте вокруг оси x на угол φ:

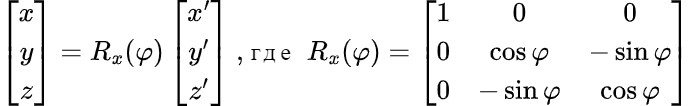
Полная матрица вращения платформы по трём осям по отношению к базе находится умножением матриц:

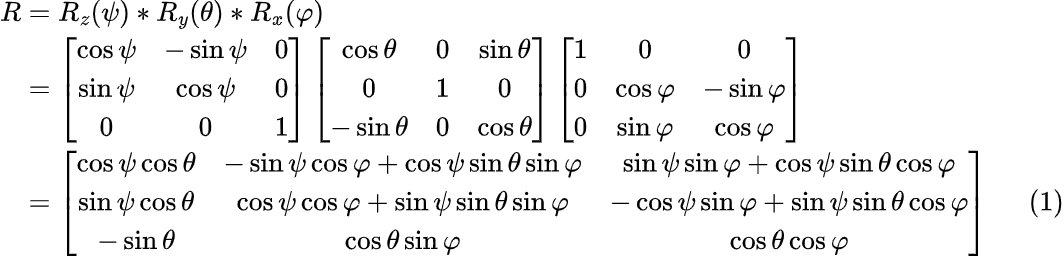
У платформы Стюарта шесть ног. Рассмотрим произвольную ногу.

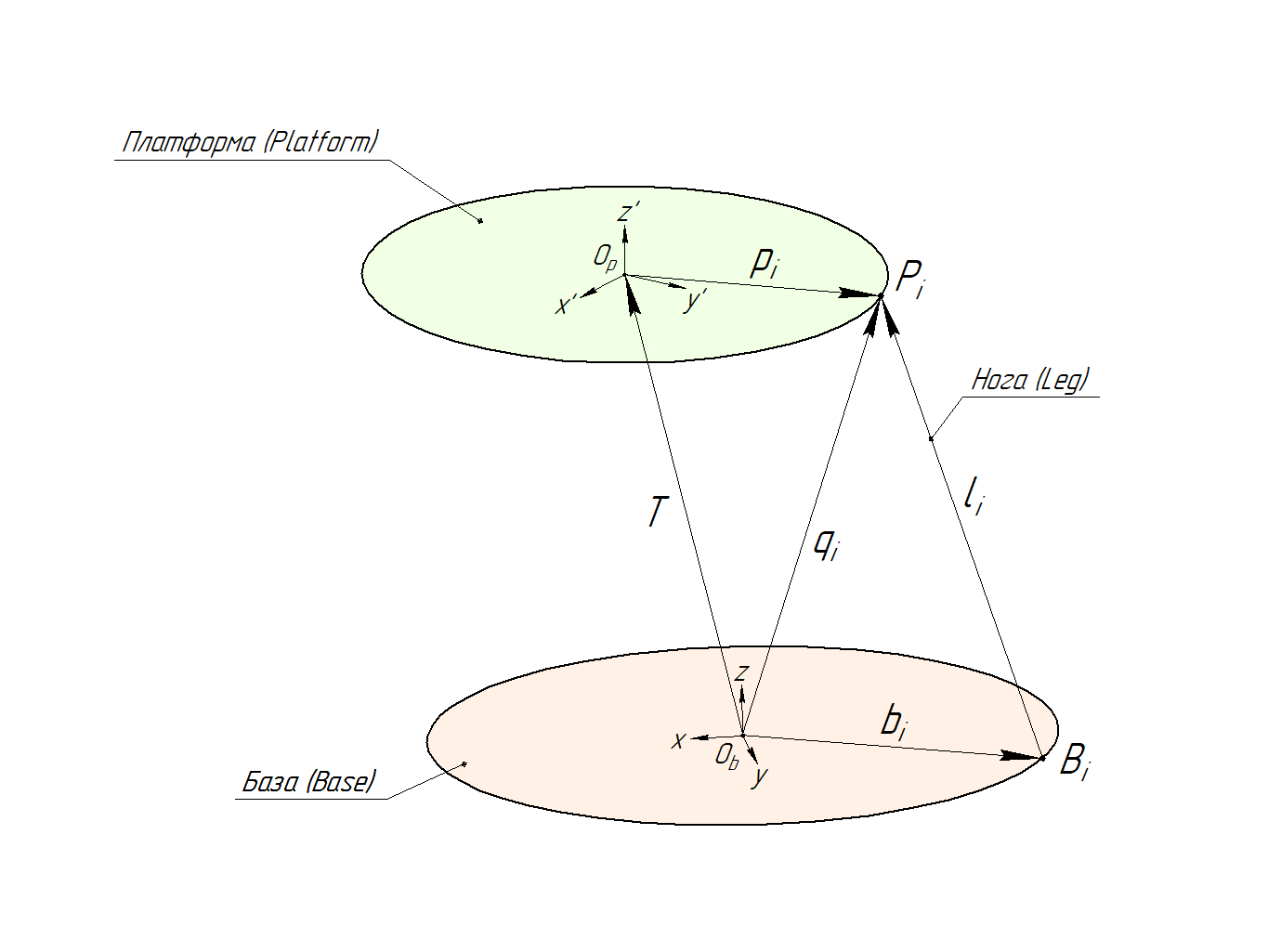
Введём обозначения:

• P_i — точка крепления ноги к платформе.
• p_i — вектор, определяющий координаты точки P_i в системе координат платформы O_p.
• B_i — точка крепления ноги к базе.
• b_i — вектор, определяющий координаты точки B_i в системе координат базы O_b.
• l_i — нога, вектор в системе координат базы O_b с началом в точке B_i и концом в точке P_i.
• T — вектор линейного перемещения центра системы координат платформы O_p в системе координат базы O_b.
• q_i — вектор, определяющий координаты точки P_i в системе координат базы O_b.

Зная линейные перемещения платформы относительно базы — T и матрицу вращения платформы — R, мы можем определить координаты вектора q_i:

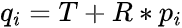
Наконец, мы можем найти координаты вектора l_i в системе координат базы O_b, зная координаты точек его начала и конца. Координаты находятся вычитанием координат начала вектора из координат конца.

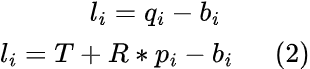
В случае с линейными приводами этого было бы достаточно. Но мы собираемся использовать поворотные приводы, что усложняет задачу. Поворотный привод может иметь любую конструкцию, но для примера мы возьмём произвольный хобби-сервопривод.

Рассмотрим схему с сервоприводом для произвольной ноги.

Введём новые обозначения и вспомним часть предыдущих:

• l_i — произвольная нога.
• d_i — ось вращения вала сервопривода.
• a_i — длина рычага сервопривода.
• s_i — длина тяги.
• P_i — точка крепления ноги к платформе и крепления тяги к платформе.
• B_i — точка крепления ноги к базе.
• A_i — точка крепления тяги к рычагу.

Рассмотрим схему подробнее. На базе находится сервопривод. На валу сервопривода жёстко закреплён рычаг (качалка) фиксированной длины a. Рычаг сервопривода вращается вокруг оси d, изображённой на схеме красным цветом. Плоскость вращения рычага выделена на схеме жёлтым цветом. При этом ось вращения рычага d лежит в плоскости базы. Таким образом, плоскость вращения рычага и плоскость базы перпендикулярны. В действительности ось вращения d может и не лежать в плоскости базы, а быть произвольной в пространстве, но это усложнит расчёты, поэтому мы используем этот частный случай.

К рычагу одним концом прикреплена тяга фиксированной длины s. Другой конец тяги прикреплён к платформе. Точки крепления тяги к рычагу сервопривода и платформе представляют собой универсальные шарниры. Таким образом, вращая вал сервопривода, мы можем изменять длину ноги l.

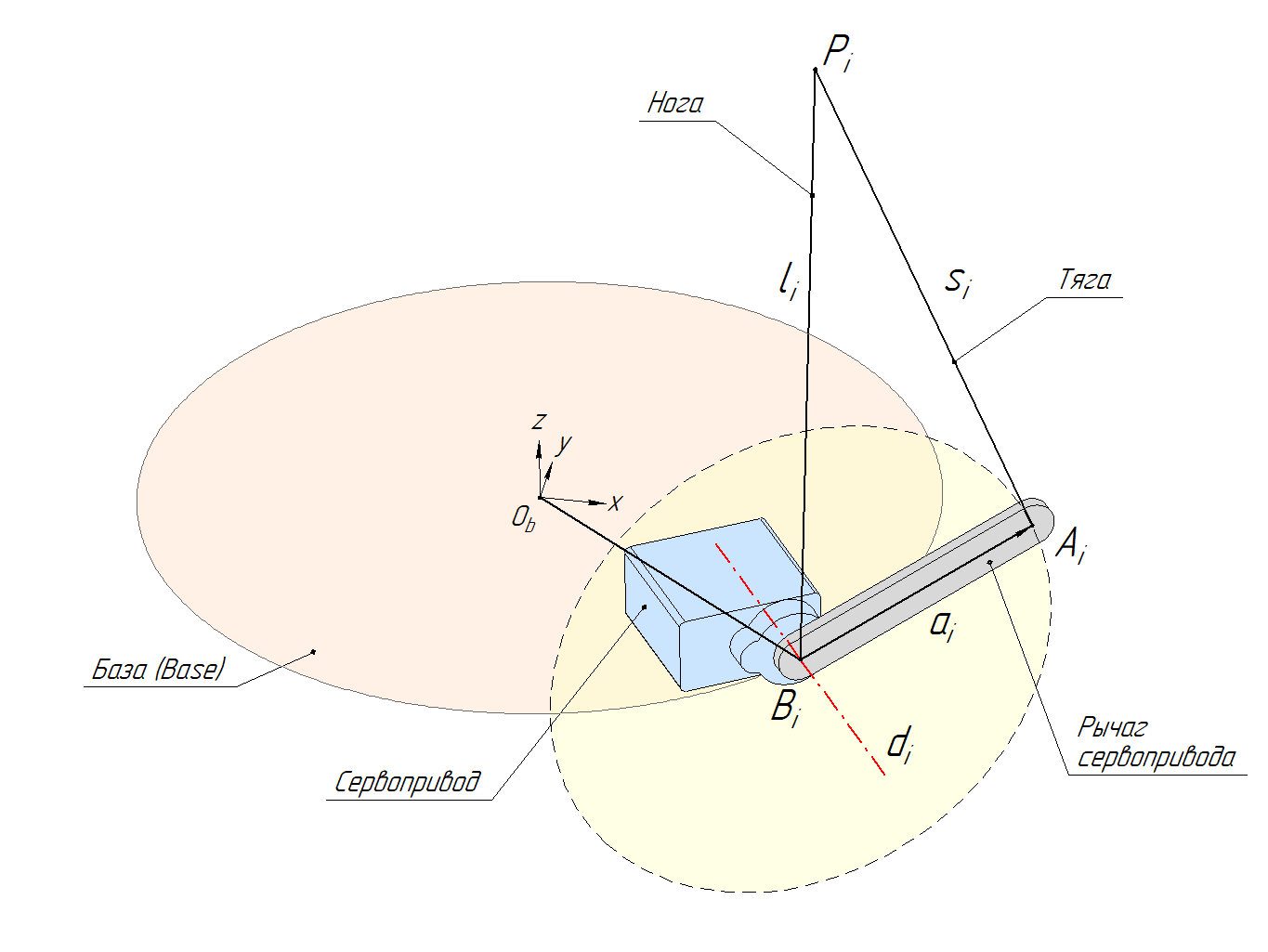
Суть задачи — найти правильный угол поворота рычага сервопривода, зная необходимую нам длину ноги l.

Назовём искомый угол α (альфа). Исходной будем считать ту позицию, в которой рычаг A₀ лежит в плоскости базы, то есть горизонтально. Также введём координаты интересующих нас точек. Пусть точка B имеет координаты (x_b, y_b, z_b), точка A имеет координаты (x_a, y_a, z_a), а P координаты (x_p, y_p, z_p). Координаты всех точек находятся в нашей главной системе координат базы O_b.

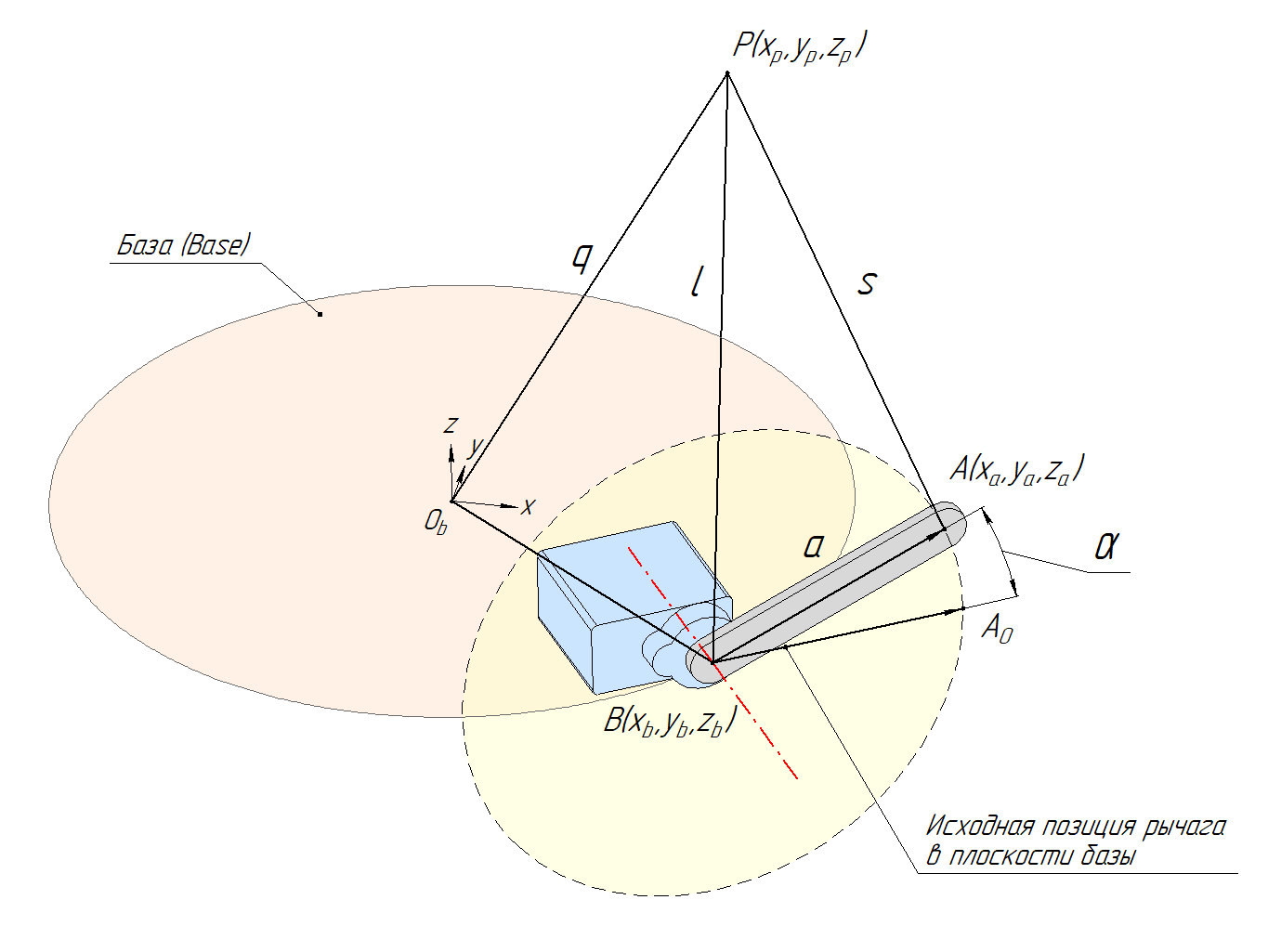
Для расчёта нам понадобится ещё один угол, который будет описывать положение плоскости вращения рычага сервопривода. За ориентир возьмём ось x в системе координат базы O_b. Назовём этот угол между осью х базы и плоскостью вращения рычага углом β (бета).

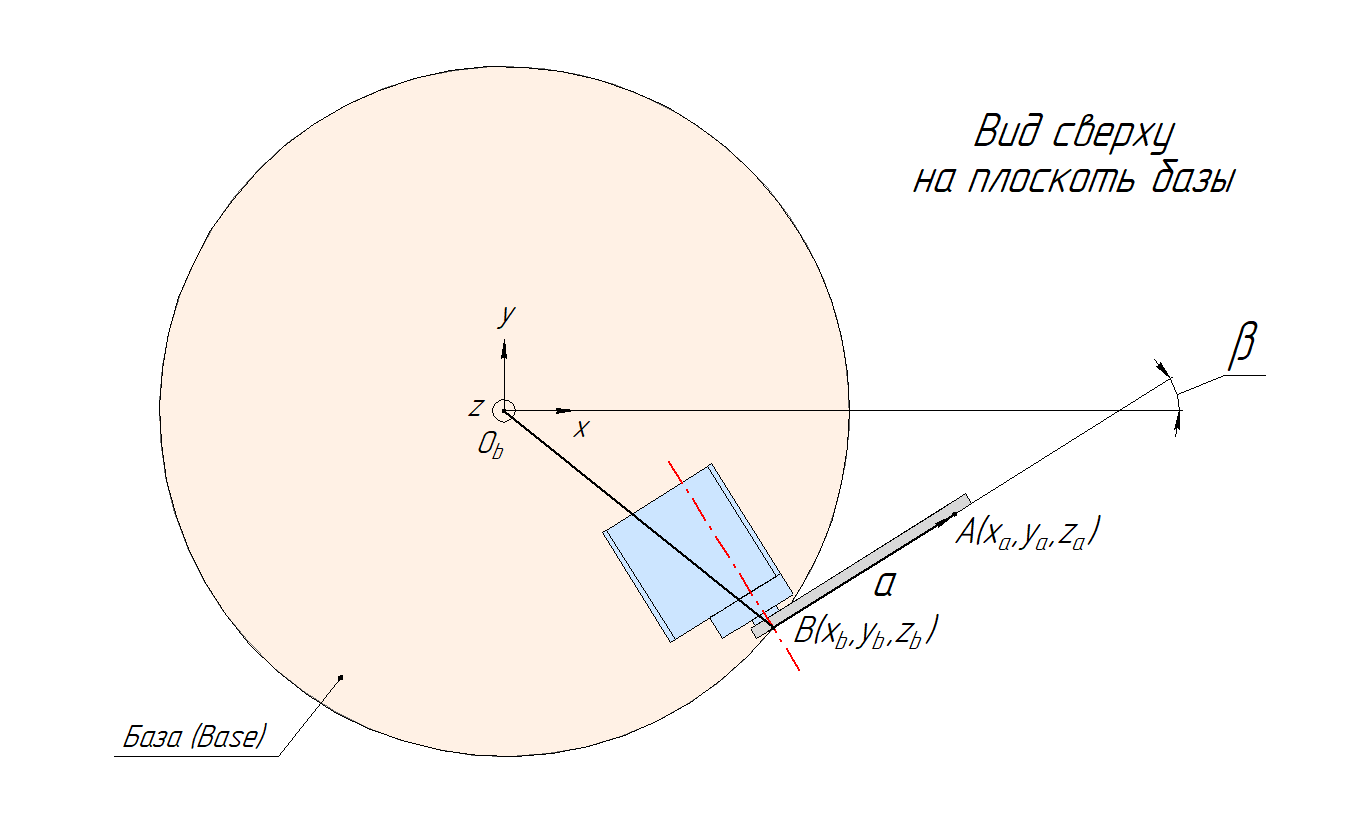
Сперва выразим координаты (x_a, y_a, z_a) для точки A на конце рычага. Как их найти? Представим, что рычаг сервопривода начинается не в точке В, а в начале координат O_b. Выполнив перенос начала вектора a из точки B в начало координат, можно обнаружить, что точка A по сути выполняет два последовательных поворота:

1. Поворот на угол α вокруг оси x.
2. Поворот на угол β вокруг оси z.

Используя уже известные нам матрицы поворота, мы можем определить результирующую матрицу поворота точки А:

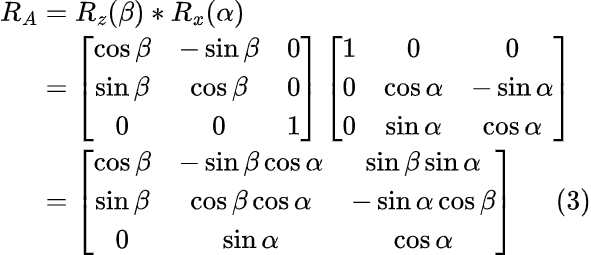
Так как исходная позиция рычага находится в плоскости базы, исходные координаты точки A до поворота можно представить в виде (0, a, 0). Приложим к исходной точке матрицу поворота R_A, а затем вернём начало вектора a из начала координат в точку B, совершив перенос. В итоге получаем следующие координаты точки A:

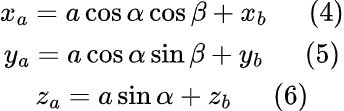
Идём далее. Следующий шаг — выразить длины векторов a, l, s через координаты. Квадрат длины вектора равен сумме квадратов его координат. Используя эту формулу, выразим длину вектора а:

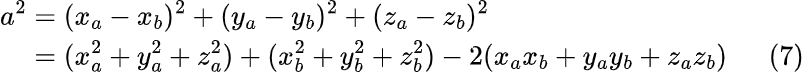
То же самое проделаем с вектором l:

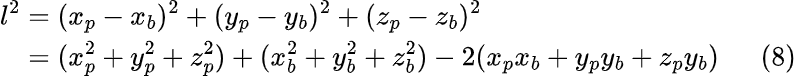
И с вектором s:

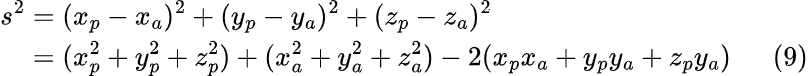
Вычтем из уравнения (9) уравнение (7):

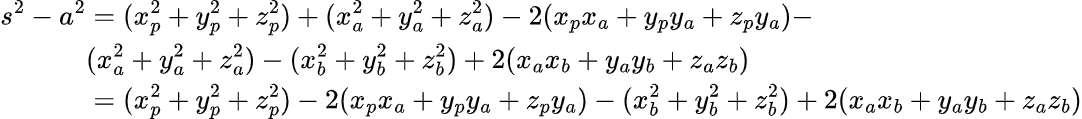
Получившееся уравнение вычтем из уравнения (8):

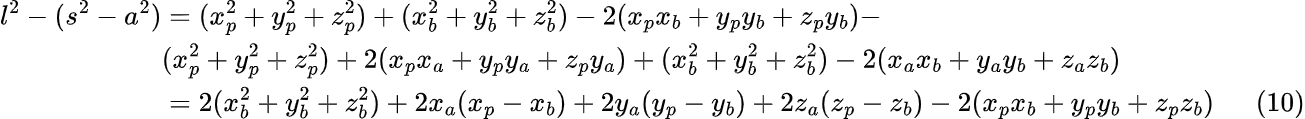
В уравнении (10) заменим координаты x_a, y_a, z_a на соответствующие уравнения (4), (5) и (6). Затем максимально упростим полученное равенство:

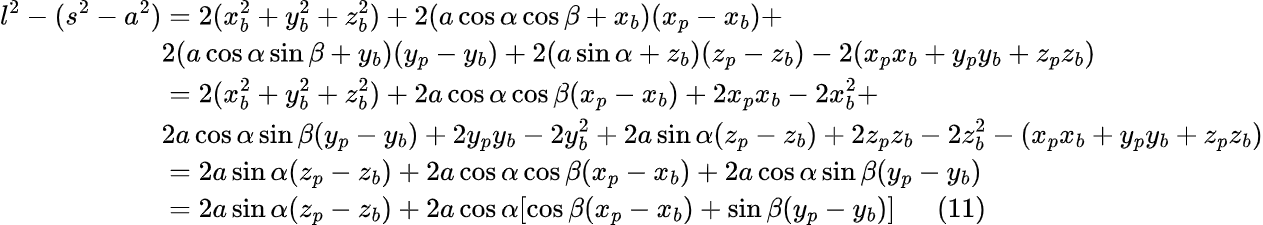
Изучив равенство (11), можно прийти к выводу, что оно похоже на тригонометрическое тождество вспомогательного аргумента формулы сложения гармонических колебаний, которое имеет вид:

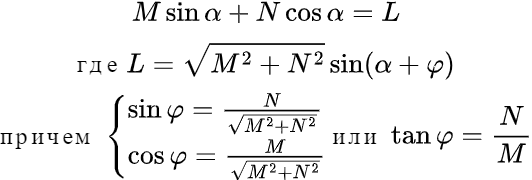
Используя это тождество, можно выразить необходимый нам угол α через параметры M, N, и L:

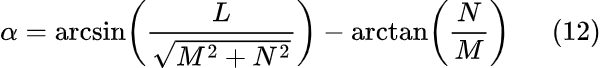
Сами же параметры M, N, и L возьмём из равенства (11):

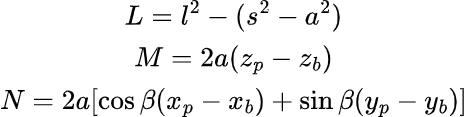
Готово! Мы выразили искомый угол рычага сервопривода α через векторы l, s, a и координаты точек P, B. Этих данных достаточно для создания программы симуляции.

Симуляция платформы Стюарта

Симуляция — крайне полезный этап разработки в робототехнике. Поэтому, прежде чем воплощать реальную платформу Стюарта «в железе», сделаем её симуляцию. Она позволит нам не только проверить математическую модель, описанную выше, но и подобрать нужные размеры платформы до её конструирования.

В качестве исходников для нашей программы симуляции используем код из проекта memememe за авторством Radames Ajna и Thiago Hersan.

Программа будет иметь графическую составляющую, а написана будет в среде Processing на упрощённом языке Java. Среда Processing очень популярна в мире DIY, поскольку позволяет быстро создавать интерактивные графические приложения и связать их с Arduino.

Скачиваем среду разработки Processing и устанавливаем её на персональный компьютер. Processing можно установить на компьютер с любой операционной системой, в том числе на микрокомпьютер Raspberry Pi.

Весь исходный код этого проекта мы разместили в репозитории stewart-platform.

Далее не будем подробно описывать весь код и особенности создания графических приложений в Processing, а лишь рассмотрим ключевые моменты. Подробную информацию о создании 3D-графики в Processing вы найдёте в документации.

Проект Processing в репозитории называется stewart_platform_simulation.

Сперва создадим файл stewart_platform.pde, в котором будет храниться математическое описание нашей платформы. Создадим в файле новый класс Platform.

class Platform {
  private final float BASE_ANGLES[] = {-50, -70, -170, -190, -290, -310};
  private final float PLATFORM_ANGLES[] = {-54, -66, -174, -186, -294, -306};
  private final float BETA[] = {PI / 6, -5 * PI / 6, -PI / 2, PI / 2, 5 * PI / 6, -PI / 6};
  private final float BASE_RADIUS = 76;
  private final float PLATFORM_RADIUS = 60;
  private final float HORN_LENGTH = 40;
  private final float ROD_LENGTH = 130;
  private final float INITIAL_HEIGHT = 120.28183632;

  private PVector[] b, p, q, l, a;
  private PVector T, R, initial_height;
  private float[] alpha;
}

Вводим константы, описывающие главные конструктивные элементы плафтормы:

• BASE_ANGLES — углы, определяющие точки B_i, то есть точки крепления ног к базе. Угол между вектором b_i и осью x в системе координат базы O_b.
• PLATFORM_ANGLES — углы, определяющие точки P_i, то есть точки крепления ног к платформе. Угол между вектором p_i и осью x в системе координат платформы O_p.
• BETA — углы β. Угол между осью х базы и плоскостью вращения рычага сервопривода.
• BASE_RADIUS — радиус базы.
• PLATFORM_RADIUS — радиус платформы.
• HORN_LENGTH — длина рычага привода a.
• ROD_LENGTH — длина тяги s.
• INITIAL_HEIGHT — начальная высота платформы. Расстояние от O_b до O_p, когда рычаги приводов горизонтальны, а вектор a лежит в плоскости базы.

Все размеры платформы и базы будем считать в миллиметрах.

Ещё нам понадобятся переменные b, p, q, l, a типа PVector, которые определяют соответствующие вектора из математического описания. Этим же типом вводим вектор линейного перемещения платформы относительно базы T, вектор вращения платформы R и вектор initial_height, описывающий исходное положение платформы относительно базы. В массиве alpha будем хранить углы вращения рычагов приводов.

При инициализации класса Platform выделяем память под все наши переменные:

public Platform() {
  T = new PVector();
  R = new PVector();
  b = new PVector[6];
  p = new PVector[6];
  q = new PVector[6];
  l = new PVector[6];
  a = new PVector[6];
  alpha = new float[6];

  initial_height = new PVector(0, 0, INITIAL_HEIGHT);

  for (int i = 0; i < 6; i++) {
    float xb = BASE_RADIUS * cos(radians(BASE_ANGLES[i]));
    float yb = BASE_RADIUS * sin(radians(BASE_ANGLES[i]));
    b[i] = new PVector(xb, yb, 0);

    float px = PLATFORM_RADIUS * cos(radians(PLATFORM_ANGLES[i]));
    float py = PLATFORM_RADIUS * sin(radians(PLATFORM_ANGLES[i]));
    p[i] = new PVector(px, py, 0);

    q[i] = new PVector(0, 0, 0);
    l[i] = new PVector(0, 0, 0);
    a[i] = new PVector(0, 0, 0);
  }
  calculateVectorQL();
}

Здесь же мы высчитываем вектор initial_height, зная исходную высоту платформы относительно базы. Для каждой ноги платформы высчитываем векторы b и p, зная радиусы платформы и базы, а также углы до точек соединений ног.

После инициализации для каждой ноги считаем вектор q и вектор l. За это отвечает функция calculateVectorQL:

private void calculateVectorQL() {
  for (int i = 0; i < 6; i++) {
    // Apply rotation
    q[i].x = cos(R.z) * cos(R.y) * p[i].x
        + (-sin(R.z) * cos(R.x) + cos(R.z) * sin(R.y) * sin(R.x)) * p[i].y
        + (sin(R.z) * sin(R.x) + cos(R.z) * sin(R.y) * cos(R.x)) * p[i].z;

    q[i].y = sin(R.z) * cos(R.y) * p[i].x
        + (cos(R.z) * cos(R.x) + sin(R.z) * sin(R.y) * sin(R.x)) * p[i].y
        + (-cos(R.z) * sin(R.x) + sin(R.z) * sin(R.y) * cos(R.x)) * p[i].z;

    q[i].z = -sin(R.y) * p[i].x + cos(R.y) * sin(R.x) * p[i].y
        + cos(R.y) * cos(R.x) * p[i].z;

    // Apply translation
    q[i].add(PVector.add(T, initial_height));

    // Obtain l vector
    l[i] = PVector.sub(q[i], b[i]);
  }
}

Делаем это ровно тем же способом, что и в математической модели. Сперва вектор p умножаем на полную матрицу вращения платформы по трём осям R. Затем прибавляем вектор линейного перемещения T, вектор начального положения платформы initial_height и получаем вектор q. Зная векторы q и b, через разницу координат находим вектор l.

Наконец, посчитаем углы вращения рычагов alpha для каждой ноги. За это отвечает функция calculateAngleAlpha:

private void calculateAngleAlpha() {
  for (int i = 0; i < 6; i++) {
    float L = l[i].magSq() - ((ROD_LENGTH * ROD_LENGTH) - (HORN_LENGTH * HORN_LENGTH));
    float M = 2 * HORN_LENGTH * (q[i].z - b[i].z);
    float N = 2 * HORN_LENGTH * (cos(BETA[i]) * (q[i].x - b[i].x) + sin(BETA[i]) * (q[i].y - b[i].y));
    alpha[i] = asin(L / sqrt(M * M + N * N)) - atan2(N, M);

    // Obtain a vector
    a[i].set(HORN_LENGTH * cos(alpha[i]) * cos(BETA[i]) + b[i].x,
        HORN_LENGTH * cos(alpha[i]) * sin(BETA[i]) + b[i].y,
        HORN_LENGTH * sin(alpha[i]) + b[i].z);
  }
}

Как и прежде, просто следуем математической модели. Высчитываем параметры L, M, N из формулы гармонических колебаний, а затем через них считаем угол α. Помимо этого для визуализации высчитаем и вектор a.

Математика готова! Добавим нашему классу метод для задания вектора линейного смещения T и вектора поворота R. Назовём его applyTranslationAndRotation. Теперь, передавая в эту функцию желаемое отклонение платформы от базы, мы получим шесть нужных углов привода.

public void applyTranslationAndRotation(PVector translation, PVector rotation) {
  R.set(rotation);
  T.set(translation);
  calculateVectorQL();
  calculateAngleAlpha();
}

Остальные функции и методы, оставшиеся в файле stewart_platform.pde, мы описывать не будем. Все они служат для отрисовки графических примитивов. Мы визуализируем платформу и базу как два эллипса (ellipse), рычаги и тяги как линии (line()), а сочленения обозначим жирными точками (point()). Также для удобства мы нарисовали системы координат платформы и базы, в которых оси x соответствует красный цвет, оси y зелёный, а оси z — синий.

Создадим второй файл Processing с названием stewart_platform_simulation_control.pde, который будет точкой входа нашего приложения. Подробно расписывать его тоже не будем, а отметим главное, вы можете изучить Processing самостоятельно. Камера и её управление реализованы через библиотеку PeasyCam, а элементы управления, такие как слайдеры и кнопки, сделаны библиотекой ControlP5.

При работе с 3D-графикой в среде Processing есть важная особенность. В режиме 2D-графики точка с координатой (0, 0) находится в верхнем левом углу приложения, ось x направляется вправо, а ось y вниз. При переходе в 3D это даёт левостороннюю систему координат, в то время как весь инженерный мир привык к правосторонней. С этим у вас может возникнуть путаница, так как при разработке реальной конструкции мы будем пользоваться именно правосторонней системой координат.

Пример работы приложения:

Расскажем в общих чертах, как работает приложение.

Положение камеры относительно платформы Стюарта регулируется мышкой.

В левом верхнем углу мы сделали шесть слайдеров. Три верхних слайдера задают линейное отклонение платформы относительно базы по трём осям, то есть вектор T. Размеры нашей платформы указаны в миллиметрах, поэтому отклонения задаём тоже в миллиметрах. Три следующих слайдера задают поворот платформы относительно базы по трём осям, то есть вектор R. Углы поворота задаём в радианах.

Чуть ниже слайдеров мы разместили кнопку сброса RESET для сброса платформы в исходное состояние, при котором положение рычагов приводов горизонтально, а сами рычаги находятся в плоскости базы.

Ниже кнопки сброса мы вывели текущие значения шести углов α для шести поворотных приводов соответственно. Ещё для удобства вывели текущие Roll, Pitch, и Yaw платформы в градусах.

Изменяя положения слайдеров, вы увидите соответствующие отклонения платформы от базы. Играя со слайдерами, вы сможете подобрать нужные вам значения BASE_ANGLES, PLATFORM_ANGLES, BETA, BASE_RADIUS, PLATFORM_RADIUS, HORN_LENGTH и ROD_LENGTH.

Также благодаря симуляции вы можете определить физические границы движения платформы. Например, на видео видно, какие значения линейного перемещения платформы вверх-вниз являются максимальными и минимальными. При невозможном построении кинематической цепи проблемные элементы перестанут рендериться, а в значении угла поворота привода появится значение NaN.

Дизайн и конструирование платформы

После симуляции мы прикинули желаемые размеры платформы Стюарта и её деталей, а значит, пришло время заняться конструированием.

3D-модель нашей платформы, как и весь исходный код этого проекта, мы разместили в репозитории stewart-platform.

Первым делом нужно определиться с теми деталями, которые слишком редки, и мы не сможем их заказать или сделать самостоятельно. В нашем случае это универсальные шарниры. Шарниры должны быть миниатюрные, поскольку сама платформа Стюарта будет маленькой.

На помощь, как всегда, приходят запчасти для радиоуправляемых машинок. В качестве универсальных шарниров мы выбрали шариковые наконечники рулевых тяг Traxxas TRA5347. Эти рулевые наконечники можно найти и на российских маркетплейсах. В наборе двенадцать шариковых наконечников — ровно столько, сколько нам нужно: шесть шарниров на платформу и шесть шарниров на рычаги.

Никаких геометрических размеров от Traxxas, разумеется, нет, поэтому деталируем самостоятельно. Приблизительные размеры наконечников:

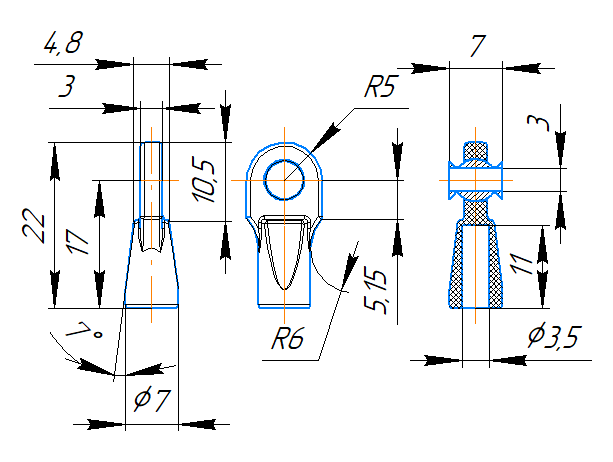
Наконечники сделаны из твёрдой резины и имеют посадочное отверстие диаметром примерно 3,5 мм. Нам нужно выбрать, на что именно их устанавливать, то есть что будет являться для них тягой. Можно взять металлический стержень с резьбой М4 и вкрутить его в наконечник. Или же можно использовать стержень диаметром 3 мм и вклеить его в наконечник, либо установить через какой-нибудь переходник.

Мы решили использовать карбоновый стержень диаметром 3,5 мм. На маркетплейсе мы нашли пультрузионный круглый карбоновый пруток диаметром 3,5 мм и длиной 1 м. Одного метра прутка с лихвой хватит на шесть не слишком длинных тяг.

По итогам симуляции мы выбрали длину тяги в 130 мм. В математическом описании длина тяги — это расстояние от одного универсального шарнира до другого. Значит, нужные нам 130 мм будем считать между центрами шариков наконечников. Из геометрии наконечников следует, что нам нужно шесть стержней длиной примерно 118 мм.

Нарезаем стержни нужной длины. Карбоновый пруток можно грубо разрезать простыми ножницами. Для достижения более точного размера мы использовали самый дешёвый труборез, он отлично пилит карбон.

Вставляем стержни в наконечники. Если стержень болтается в наконечнике, можно немного «распушить» его конец, сделав небольшой продольный разрез, тогда посадка будет плотнее.

Теперь займёмся платформой.

Платформа должна представлять собой нечто плоское и прочное. Ещё платформа должна быть лёгкой, ведь от этого будет зависеть грузоподъёмность всей конструкции и требования к мощности приводов. Исходя из формы наконечников, устанавливать их придётся в боковую поверхность платформы. У шариковых наконечников посадочное отверстие диаметром 3 мм, значит фиксировать их будем винтами М3.

Мы подумали, что лучшим решением будет напечатать каркас платформы на 3D-принтере. Это проще, чем сверлить трёхмиллиметровые отверстия в торце пластика или фанеры.

После симуляции мы выбрали для себя следующие размеры платформы.

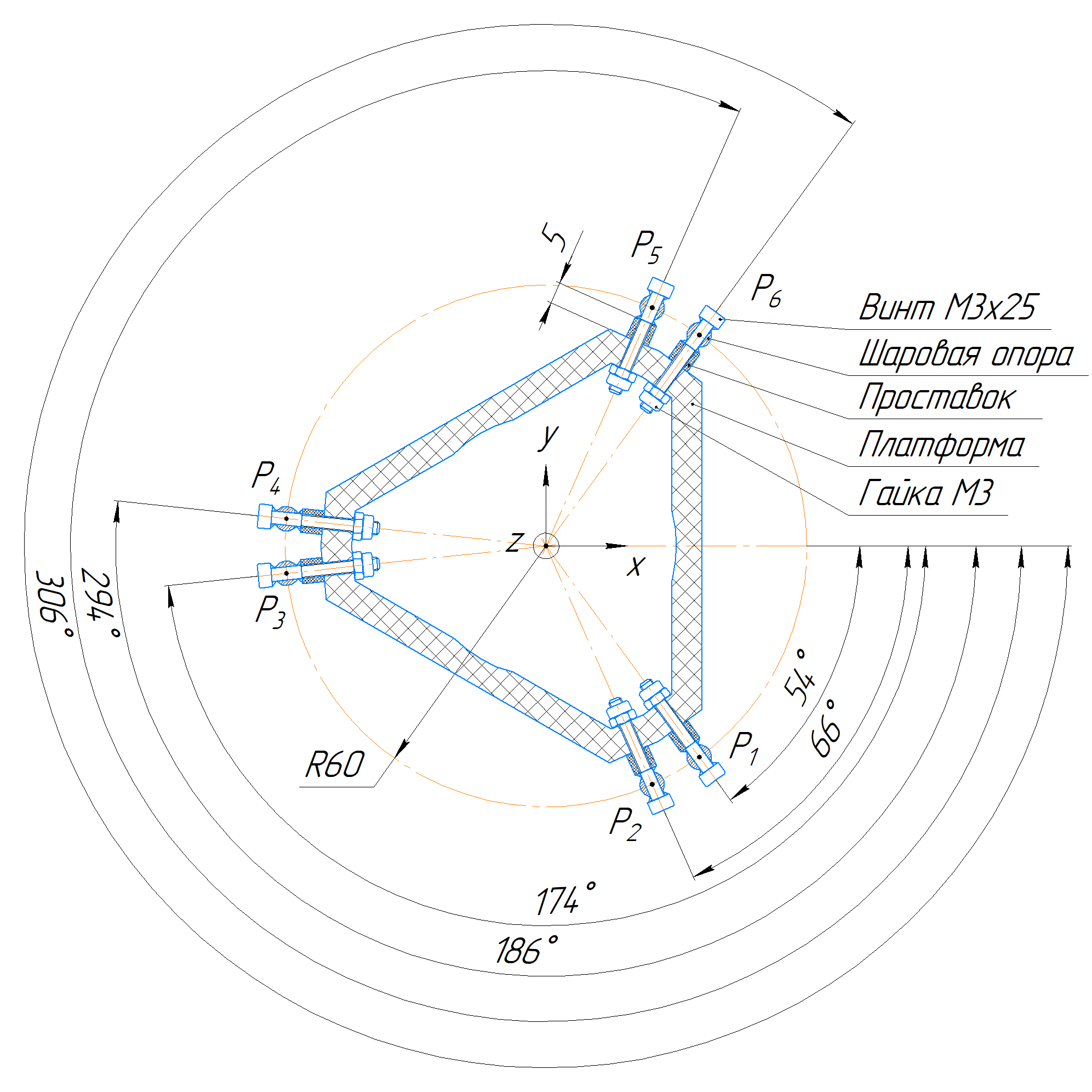
Нумерацию ног будем вести от оси x по часовой стрелке. Углы ног платформы равны 54, 66, 174, 186, 294, и 306°. Углы откладываем от оси x.

Радиус платформы — 60 мм. Обратите внимание, это радиус до универсальных шарниров, то есть расстояние от центра до точки P_i платформы. В нашем случае это расстояние от центра платформы до центра шарика наконечника тяги.

Наконечнику тяги нужно обеспечить свободный ход вокруг шара, и не стоит прижимать его вплотную к платформе. Для этого мы решили сделать небольшие проставки высотой 5 мм. Сами наконечники мы закрепим на платформе винтами и гайками М3. Гайки используем с нейлоновыми вставками, чтобы ничего не болталось и без заморочек с гровером.

Печатаем нашу детальку из PLA-пластилка, хотя материал не сильно важен.

Проставки высотой 5 мм мы решили сделать с помощью лазерной резки Figuro. Просто вырезаем небольшие колечки из листа чёрного пластика толщиной 5 мм.

Прикрутим наконечники с тягами к платформе и посмотрим, что получилось.

Теперь займёмся базой.

Здесь главный вопрос заключается в выборе поворотного привода. Мы провели эксперименты с разными приводами и выделили для себя три главных критерия выбора: точность позиционирования вала, люфт (Backlash) вала и крутящий момент. Неточное позиционирование вала и люфт в сумме дают огромную ошибку в положении платформы.

Сперва мы попробовали микросервоприводы Feetech FS90. Но они для данного проекта совсем не подходят: средний люфт, низкая точность и низкий крутящий момент. Затем мы попробовали шаговые двигатели 28BYJ-48 5V. У этих шаговиков достаточный крутящий момент, но слишком большой люфт редуктора. Мы надеялись выиграть на точности, ведь в характеристиках заявлено 2048 шагов, но постоянные пропуски шагов накапливали ошибку и нивелировали эту точность.

В итоге мы решили остановиться на сервоприводах Feetech FS5109M c металлическими шестернями. Как и большинство сервоприводов этого типа, они не могут похвастаться точностью. Но у этой модели почти отсутствует люфт, а крутящего момента нам хватит с головой.

Вы можете попробовать построить платформу Стюарта с любыми приводами, но помните: чем точнее приводы, тем качественнее проект.

Если планируете использовать сервоприводы, старайтесь, чтобы они были максимально однородные: одной марки, одной партии, одной скорости и так далее. Любая разница в поведении сервоприводов приведёт к ошибкам в позиционировании.

Мы попарно закрепили шесть сервоприводов на трёх боковых пластинах толщиной 3 мм. Боковые пластины зажали сверху и снизу ещё двумя трёхмиллиметровыми пластинами, стянутыми между собой резьбовыми стойками М3. Получилась простая конструкция из пяти однородных листовых деталей, которые можно вырезать на лазерном станке.

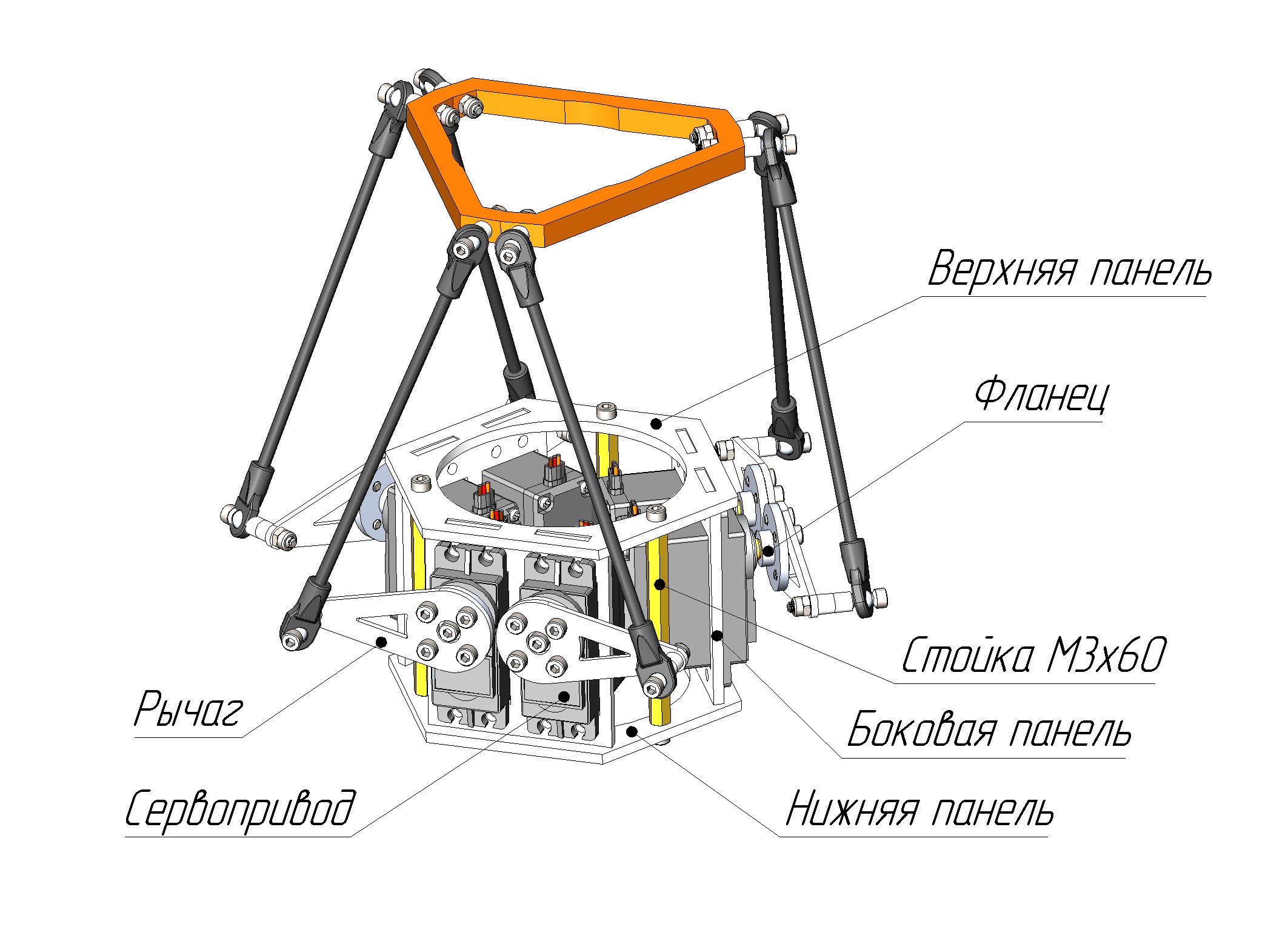
Рычаги для сервоприводов мы тоже решили сделать лазерной резкой. Но на этот раз из пластика толщиной 2 мм. Прикрепим рычаг к валу сервопривода через алюминиевый фланец.

Теперь о размерах и углах базы. После симуляции мы выбрали для себя следующие размеры:

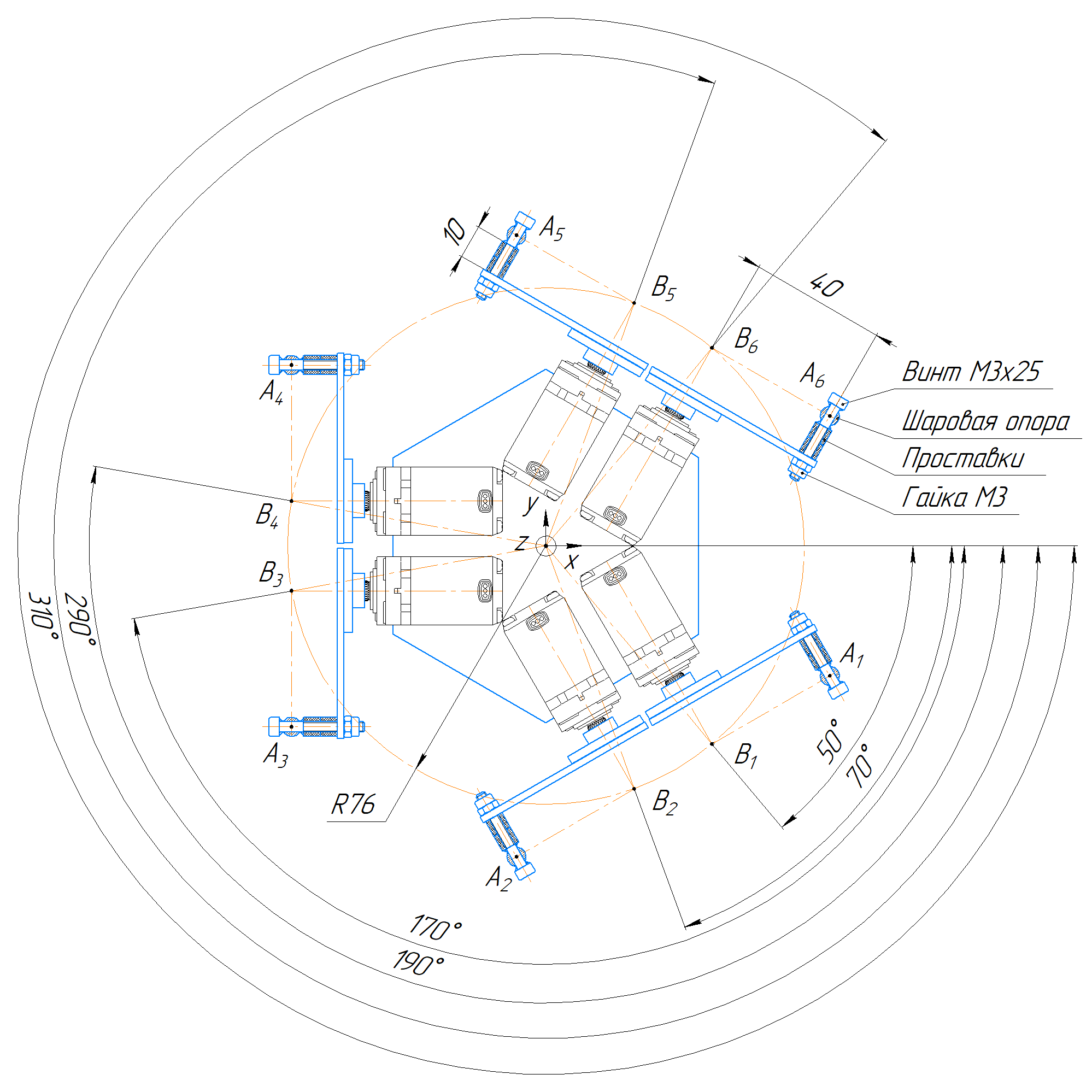
Как и на платформе, нумерация ног идёт от оси x по часовой стрелке. Углы ног базы равны 50, 70, 170, 190, 290, и 310°. Углы откладываем от оси x.

Длина рычага — 40 мм. Радиус базы — 76 мм. Обратите внимание, как именно считается радиус. В нашем случае радиус — это расстояние от центра базы до точки B_i, которая лежит на пересечении оси сервопривода и оси шаровой опоры наконечника, параллельной рычагу.

Как и в случае с платформой, наконечникам тяг на базе тоже нужно добавить свободного хода даже больше, чем на платформе. Поэтому добавляем по две проставки высотой 5 мм на конце каждого рычага. Наконечник тяги закрепляем на рычаге тем же винтом и гайкой М3.

Не забудем и об углах β. Напомним, это углы между осью x и плоскостью вращения рычага привода.

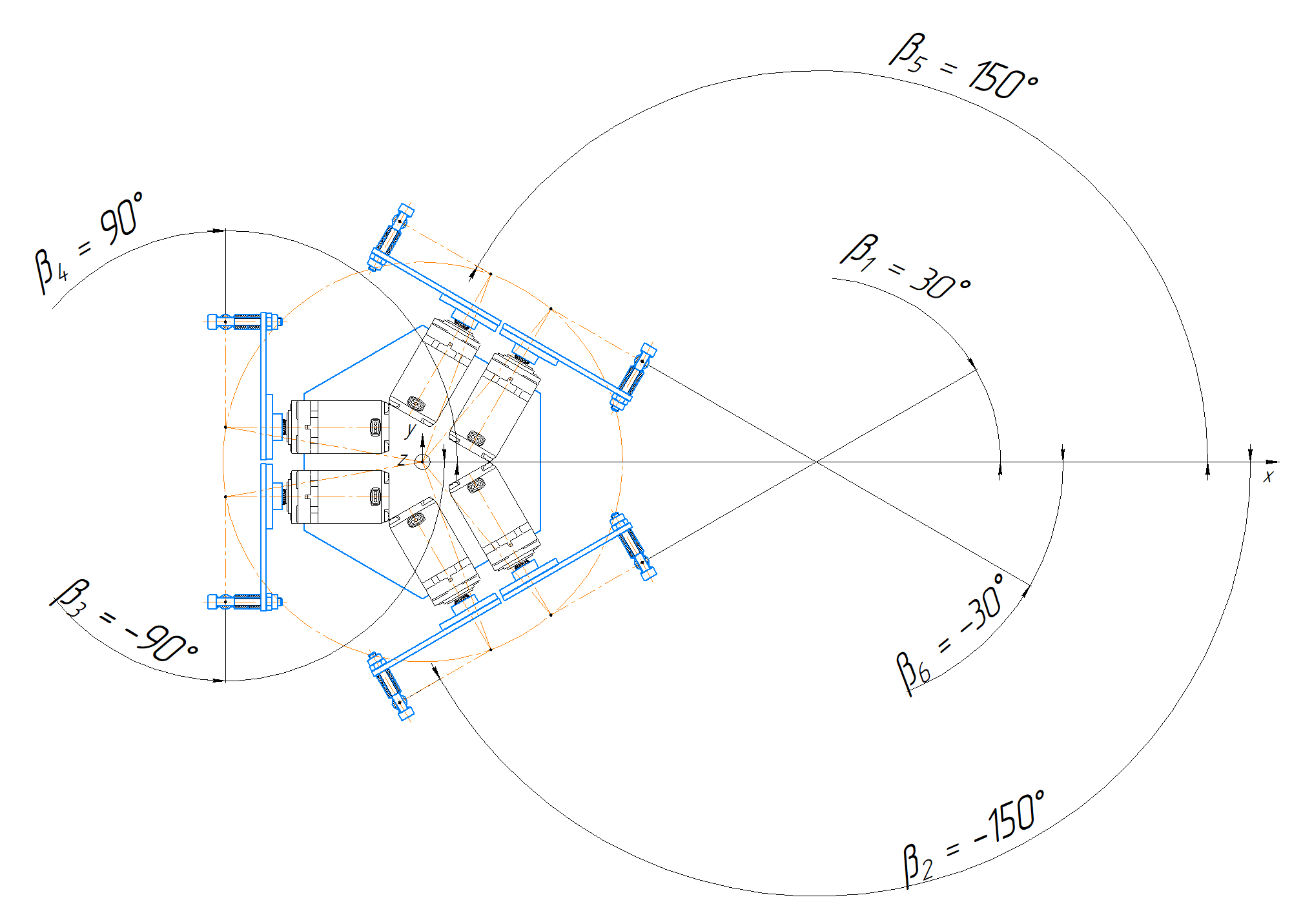
Положительный угол или отрицательный — зависит от того, как направлен рычаг сервопривода относительно оси x. Наши углы β для шести ног равны 30, −150, −90, 90, 150, и 30°.

Чтобы быстро изготовить нужные детали лазерной резкой, снова воспользуемся сервисом Figuro.

Соберём нашу базу. Прикручиваем сервоприводы к боковым пластинам винтами и гайками М3. К рычагам прикручиваем фланцы, сами фланцы устанавливаем на сервоприводы. Фланцы нужно установить так, чтобы при нейтральном положении вала сервопривода рычаг был примерно горизонтален.

Стягиваем боковые пластины резьбовыми стойками.

Совмещаем платформу с базой. Готово!

Управление платформой

Разберёмся с тем, как будем управлять платформой.

В симуляции Processing у нас уже есть весь необходимый программный код. Чтобы не переносить его на другое железо, можно просто подключиться к самому приложению Processing, например, по UART. Мы сможем получать углы alpha из приложения по последовательному интерфейсу и сразу отправлять их на сервоприводы.

С этой задачей справится буквально любой микроконтроллер, например классическая Arduino Uno. В нашем случае возьмём прямой аналог — плату Iskra Uno.

Для управления шестью сервоприводами нужно шесть ШИМ-пинов. На Iskra Uno как раз шесть пинов с функцией ШИМ, и вы можете подключить сервоприводы прямо к ней, только в этом случае придётся повозиться с разводкой питания сервоприводов. Мы не будем заморачиваться и используем готовое решение — Multiservo Shield. Останется только подключить к шилду сервоприводы и подвести питание.

Напряжение питания сервоприводов Feetech FS5109M — 4,8–6 В. Потребляемый ток — 170 мА, а ток блокировки — 2 А. Но мы не собираемся так сильно нагружать сервоприводы, поэтому и большой ток нам не нужен.

Сервоприводы решили запитать USB-блоком питания Ginzzu GA-3311UW на 5 В, 3100 мА. Напряжение 5 В укладывается в номинал для сервоприводов, а тока 3 А должно хватить за глаза. Для подводки питания к Multiservo Shield просто обрежем обычный USB-кабель. Да, не самое элегантное решение, но вполне практичное.

Модернизируем проект Processing.

В репозитории новый проект Processing называется stewart_platform_arduino.

Файл stewart_platform.pde с реализацией математики в классе Platform мы не трогаем, в нём всё остаётся как есть. А вот в файл приложения внесём изменения.

Прежде всего нам понадобится последовательный интерфейс. Для этого в Processing существует библиотека Serial. Подключаем библиотеку и создаём объект serial.

import processing.serial.*; 
Serial serial;

Методом Serial.list() можно получить список активных в данный момент UART-интерфейсов в операционной системе. В функции setup приложения открываем первый доступный интерфейс. Ставим скорость в 115200 бод.

printArray(Serial.list());
serial = new Serial(this, Serial.list()[0], 115200);

Сделаем функцию для отправки углов приводов alpha в интерфейс serial. Назовем её sendAnglesToSerial.

Чтобы отделить полезные данные от мусора, перед отправкой углов передадим пару ведущих байтов 0x6A, которые сигнализируют о том, что дальше последуют полезные данные. Все шесть углов упакуем в строку и перешлём в текстовом формате CSV.

Переменные alpha в программе имеют тип float. Большая точность мантиссы нам не нужна, ведь сервоприводы не обладают такой чувствительностью. Чтобы не заморачиваться с плавающей точкой, просто превратим float в целочисленное значение. Умножим углы на 100, округлив таким образом значение до двух знаков после запятой.

void sendAnglesToSerial() {
  byte[] cmd_bytes = { 0x6A, 0x6A };
  serial.write(cmd_bytes);
  
  String data = (int)(degrees(alpha[0]) * 100) + ","
              + (int)(degrees(alpha[1]) * 100) + ","
              + (int)(degrees(alpha[2]) * 100) + ","
              + (int)(degrees(alpha[3]) * 100) + ","
              + (int)(degrees(alpha[4]) * 100) + ","
              + (int)(degrees(alpha[5]) * 100) + "\n";
   serial.write(data);
}

В главном цикле draw приложения отправляем углы в последовательный интерфейс сразу после их получения.

  alpha = platform.getAlphaAngles();
  sendAnglesToSerial();

Теперь займёмся прошивкой Arduino.

Arduino-проект лежит в репозитории под именем stewart_platform_servos.ino. Код прошивки:

#include <Multiservo.h>

constexpr uint16_t SERVO_MIN_PULSE_WIDTH[6] = { 544 - 34, 544 + 78, 544 + 20, 544 + 0, 544 - 44, 544 - 70 };
constexpr uint16_t SERVO_MIDDLE_PULSE_WIDTH[6] = { 1522 - 48, 1522 + 60, 1522 + 0, 1522 + 14, 1522 - 28, 1522 - 116 };
constexpr uint16_t SERVO_MAX_PULSE_WIDTH[6] = { 2500 - 84, 2500 + 0, 2500 - 20, 2500 - 30, 2500 - 64, 2500 - 102 };

constexpr uint8_t MULTI_SERVO_PIN[6] = { 0, 1, 2, 3, 4, 5 };

Multiservo multiservo[6];

float target_angle_degree[6] = { 0.0, 0.0, 0.0, 0.0, 0.0, 0.0 };

void resetToZero() {
  for (uint8_t i = 0; i < 6; i++)
    multiservo[i].writeMicroseconds(SERVO_MIDDLE_PULSE_WIDTH[i]);
}

void servosHandler() {
  for (uint8_t i = 0; i < 6; i++) {
    uint16_t pulse = 0;
    if (target_angle_degree[i] >= 0)
      pulse = map(target_angle_degree[i], 0.0, 90.0, SERVO_MIDDLE_PULSE_WIDTH[i], SERVO_MAX_PULSE_WIDTH[i]);
    else if (target_angle_degree[i] < 0)
      pulse = map(target_angle_degree[i], -90.0, 0.0, SERVO_MIN_PULSE_WIDTH[i], SERVO_MIDDLE_PULSE_WIDTH[i]);
    multiservo[i].writeMicroseconds(pulse);
  }
}

void setup() {
  Serial.begin(115200);

  for (uint8_t i = 0; i < 6; i++)
    multiservo[i].attach(MULTI_SERVO_PIN[i]);

  resetToZero();
}

void loop() {
  if (Serial.available()) {
    if (Serial.read() == 0x6A && Serial.read() == 0x6A) {
      for (uint8_t i = 0; i < 6; i++) {
        target_angle_degree[i] = (float)Serial.parseInt() / 100.0;
        target_angle_degree[i] = i % 2 ? -1 * target_angle_degree[i] : target_angle_degree[i];
      }
    }
  }
  servosHandler();
}

Здесь всё максимально просто. Для управления сервоприводами через Multiservo Shield используем Arduino-библиотеку Multiservo. Сервоприводы мы подключили к первым шести пинам шилда. Углы сервоприводов хранятся в массиве target_angle_degree.

Главным моментом прошивки является поднастройка позиций валов сервоприводов. Хобби-сервоприводы управляются ШИМ-сигналом с приблизительной шириной от 544 до 2500 мс с нейтральным положением в 1522 мс. Вам нужно максимально точно подогнать ширину импульса к реальным физическим углам.

• SERVO_MIDDLE_PULSE_WIDTH — угол рычага равен 0°. Рычаг горизонтален, и его вектор лежит в плоскости базы.
• SERVO_MIN_PULSE_WIDTH — угол рычага привода в −90°.
• SERVO_MAX_PULSE_WIDTH — угол рычага привода в 90°.

Мы подбирали ширину импульса на глаз, но вы можете попробовать и более точные методы.

constexpr uint16_t SERVO_MIN_PULSE_WIDTH[6] = { 544 - 34, 544 + 78, 544 + 20, 544 + 0, 544 - 44, 544 - 70 };
constexpr uint16_t SERVO_MIDDLE_PULSE_WIDTH[6] = { 1522 - 48, 1522 + 60, 1522 + 0, 1522 + 14, 1522 - 28, 1522 - 116 };
constexpr uint16_t SERVO_MAX_PULSE_WIDTH[6] = { 2500 - 84, 2500 + 0, 2500 - 20, 2500 - 30, 2500 - 64, 2500 - 102 };

void servosHandler() {
  for (uint8_t i = 0; i < 6; i++) {
    uint16_t pulse = 0;
    if (target_angle_degree[i] >= 0)
      pulse = map(target_angle_degree[i], 0.0, 90.0, SERVO_MIDDLE_PULSE_WIDTH[i], SERVO_MAX_PULSE_WIDTH[i]);
    else if (target_angle_degree[i] < 0)
      pulse = map(target_angle_degree[i], -90.0, 0.0, SERVO_MIN_PULSE_WIDTH[i], SERVO_MIDDLE_PULSE_WIDTH[i]);
    multiservo[i].writeMicroseconds(pulse);
  }
}

После запуска программы выставляем все сервоприводы в ноль — resetToZero.

Для коммуникации используем аппаратный Serial-интерфейс Arduino Uno. Если в буфере serial есть входные данные, читаем их. Если встречаем два контрольных байта 0x6A, начинаем парсить данные из формата CSV. Для этого используем метод parseInt(). Углы мы храним в том же виде, что и в приложении Processing, поэтому переводим целочисленные значения углов обратно во float, разделив их на 100.

if (Serial.available()) {
  if (Serial.read() == 0x6A && Serial.read() == 0x6A) {
    for (uint8_t i = 0; i < 6; i++) {
      target_angle_degree[i] = (float)Serial.parseInt() / 100.0;
      target_angle_degree[i] = i % 2 ? -1 * target_angle_degree[i] : target_angle_degree[i];
    }
  }
}

Готово! Подключаем Arduino к компьютеру и загружаем нашу прошивку. Запускаем приложение Processing и пробуем управлять платформой оттуда.

Платформа Стюарта работает! Точность, конечно, оставляет желать лучшего, но тем не менее математика работает. На видео можно видеть разницу в направлении некоторых движений между визуализацией и реальной платформой. Это связано с разными системами координат: в Processing она левосторонняя, а думаем мы и собираем платформу в правосторонней.

Платформа-балансир

Управлять платформой Стюарта вручную довольно скучно, придумаем ей какое-нибудь применение.

Например, на основе платформы Стюарта можно сделать балансирующую систему. Пусть наша платформа катает шарик по плоскости, не давая ему упасть. В DIY-мире Arduino это очень распространённый эксперимент, повторим его и мы.

Для определения положения шарика нам нужен датчик. Часто в подобных проектах используют видеокамеру и визуальное распознавание позиции шарика на платформе. Мы же попробуем что-нибудь попроще.

В качестве датчика положения будем использовать сенсорный экран наподобие тех, что в сенсорных панелях управления или смартфонах. Это очень подходящее для нас решение, поскольку сенсорный экран обычно сделан на стеклянной подложке, а значит, будет выполнять функции и сенсора, и самой платформы одновременно.

Существует несколько основных типов сенсорных экранов, которые работают на разных физических принципах. Мы возьмём сенсор простейшего типа — резистивный четырёхпроводной. Резистивные сенсоры совместимы с Arduino, поскольку они питаются напряжением 5 В, а для считывания сигнала нужно всего два АЦП-пина микроконтроллера.

Размеры резистивных сенсоров в основном соответствуют размерам и форматам экранов мобильных устройств и измеряются по диагонали в дюймах. Нам нужен небольшой сенсор, пропорциональный платформе.

Мы решили использовать четырёхпроводной резистивный сенсор ST-104001 с диагональю 10,4″. Этот сенсор можно приобрести не только в Китае, но и в российских интернет-магазинах.

Размеры стекла сенсорного экрана — 225×171,5 мм. Размер активной области сенсора примерно 212,2×159,4 мм. Толщина сенсора — около 1,5 мм.

Сенсорный экран подключается через миниатюрный шлейф с шагом контактов 1 мм. Подключить такой шлейф к Arduino довольно проблематично, поэтому используем специальный переходник на привычные нам BLS-контакты с шагом 2,54 мм.

Сенсор срабатывает от приложенного к нему усилия. Катать пластиковый шарик не получится: панель не будет на него реагировать, слишком маленький вес. Очевидно, шарик должен быть потяжелее. Для эксперимента мы взяли стальные шарики от подшипников разного диаметра.

Подбором мы выяснили, что сенсор начинает срабатывать на стальной шарик диаметром 18 мм и выше. Такой шарик весит примерно 26,5 граммов, то есть сенсор срабатывает от усилия примерно в четверть ньютона.

Закрепим сенсорный экран на платформе плотной посадкой с четырёх сторон.

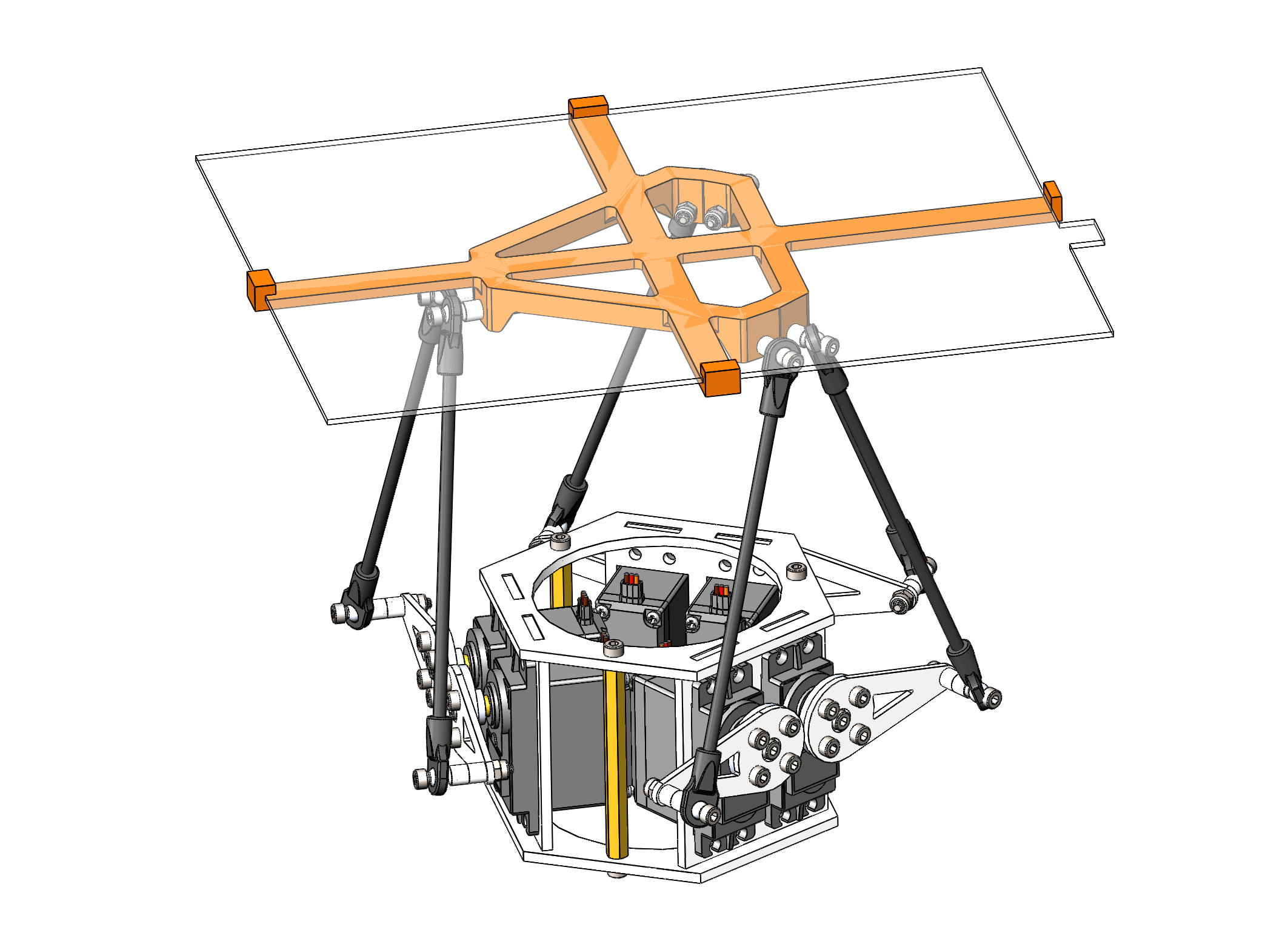
Печатаем новую деталь платформы на 3D-принтере.

Меняем деталь платформы и пересобираем девайс.

Вставляем сенсорный экран в новую платформу.

Подключаем сенсорный экран к Arduino. Для подключения используются четыре пина: два пина на ось Х (длинная сторона экрана) и два пина на ось Y. Для каждой стороны на один пин подается напряжение (плюс), а с другого пина это напряжение считывается (минус).

Провода стороны Х мы подключили к пинам 9 и А3, а стороны Y — к пинам 8 и А2.

Модифицируем Arduino-прошивку платформы. Проект с обновлённой прошивкой в репозитории называется stewart_platform_touchscreen.ino.

Для резистивных сенсорных экранов в Arduino есть библиотека TouchScreen. Включаем её в наш проект.

#include <TouchScreen.h>

constexpr uint8_t YP = A2;
constexpr uint8_t XM = A3;
constexpr uint8_t YM = 8;
constexpr uint8_t XP = 9;

constexpr float X_MIN = 75.0;
constexpr float X_MAX = 975.0;
constexpr float Y_MIN = 120.0;
constexpr float Y_MAX = 921.0;

constexpr float TOUCHSCREEN_WIDTH = 225.0;
constexpr float TOUCHSCREEN_HEIGHT = 171.5;

constexpr float BALL_BREAKTHROUGH = 50.0;

TouchScreen ts = TouchScreen(XP, YP, XM, YM, 0);

union coordinate {
  uint8_t b[2];
  int16_t i;
};

coordinate x_valid, y_valid;

Создаём объект для работы с сенсорным экраном ts. Вводим константы. Физические размеры экрана — TOUCHSCREEN_WIDTH и TOUCHSCREEN_HEIGHT в миллиметрах. Значения сенсора в крайних точках экрана — X_MIN, X_MAX, Y_MIN, Y_MAX. Их можно получить, просто ткнув пальцем в нужный край сенсора. Начало координат сенсора находится в углу экрана. В переменных x_valid и y_valid будем хранить текущее отклонение шарика в миллиметрах.

Обрабатывать позицию шарика будет приложение Processing, так как вся математика у нас содержится там. Arduino же будет просто считывать данные с сенсора и передавать их приложению по тому же UART-интерфейсу serial, что мы используем для получения углов alpha.

Для отправки данных из Arduino в Processing тоже используем пару ведущих байтов 0x6B, чтобы избавиться от случайного мусора.

При резком движении по стеклу шарик может потерять контакт с сенсором. В этот момент программа получит по последовательному интерфейсу партию нежелательных данных, что повлечёт неправильное поведение. Чтобы избавиться от внезапного резкого изменения данных, введём максимальную разницу в координатах BALL_BREAKTHROUGH в миллиметрах. Если новая полученная координата шарика отличается от старой меньше, чем на величину BALL_BREAKTHROUGH, значит шарик прокатился по панели без резких прыжков.

Кроме этого нужно определить, что именно передаёт сенсор, если на нём нет шарика. При отсутвии объекта лучше использовать последнюю позицию шарика.

В основном цикле программы:

• Опрашиваем сенсор.
• Преобразуем данные с сенсора в позицию шарика в миллиметрах.
• Преобразуем систему координат для шарика из угла сенсора в центр.
• Избавляемся от одинаковых данных, когда шарик стоит на месте.
• Избавляемся от ситуаций, когда шарика и вовсе нет.
• Проверяем новые координаты шарика на внезапный проскок.
• Отправляем готовые данные в serial следом за контрольными байтами.

TSPoint p = ts.getPoint();
float x = map(p.x, X_MIN, X_MAX, 0, TOUCHSCREEN_WIDTH);
float y = map(p.y, Y_MIN, Y_MAX, 0, TOUCHSCREEN_HEIGHT);
x = constrain(x, 0, TOUCHSCREEN_WIDTH);
y = constrain(y, 0, TOUCHSCREEN_HEIGHT);

// Смещаем систему координат в центр
x = x - TOUCHSCREEN_WIDTH / 2;
y = y - TOUCHSCREEN_HEIGHT / 2;  

// Не отправляем одинаковые координаты
if (x == x_valid.i && y == y_valid.i)
  return;  
// Если нет шарика то координаты примерно (-112, 73), отсеиваем их
if (x < -110.0) 
  return;
// Отсеиваем резкий проскок шара
if ((abs(x - x_valid.i) >= BALL_BREAKTHROUGH) || (abs(y - y_valid.i) >= BALL_BREAKTHROUGH))
  return;

x_valid.i = x;
y_valid.i = y;

Serial.write(0x6B);
Serial.write(0x6B);
Serial.write(x_valid.b, 2);
Serial.write(y_valid.b, 2);
Serial.flush();

Теперь разберёмся с приложением Processing. Это будет уже третий апгрейд нашей программы. Новая версия имеет в репозитории имя stewart_platform_balancer.

Введём новые переменные в файле приложения.

float ball_x = 0, ball_y = 0; 

В переменных ball_x и ball_y будем хранить положение шарика в миллиметрах по осям X и Y соответственно.

В среде Proceesing для чтения данных из последовательного порта лучше использовать прерывания и функцию serialEvent(). Порядок поступающих с Arduino данных от младшего к старшему (little-endian). Передаваемые кординаты имеют знаковый тип int16_t.

void serialEvent(Serial serial) {
    if ((serial.read() == 0x6B) && (serial.read() == 0x6B)) {
        ball_x = serial.read() + (serial.read() << 8);
        ball_y = serial.read() + (serial.read() << 8);
        if (ball_x > 65000) ball_x = ball_x - 65535;
        if (ball_y > 65000) ball_y = ball_y - 65535;
        //println(ball_x, " ", ball_y);
    }
}

Если в буфере последовательного интерфейса есть данные, проверяем их на наличие двух контрольных байтов 0x6B. Если всё OK, читаем координаты шарика на сенсорном экране.

Далее встаёт вопрос: как контролировать шарик?

Первым на ум приходит использовать ПИД-регулятор. Так и поступим.

Библиотеки ПИД-регулятора для Processing нет. Порывшись на просторах GitHub, мы взяли первую попавшуюся кроссплатформенную имплементацию ПИД-регулятора на Java. Просто закидываем файл с классом ПИД-регулятора в наш проект на Processing.

Всё достаточно просто. Создадим два контроллера. Один будет следить за положением шарика на оси X платформы и управлять вращением платформы вокруг оси Y (Pitch). Второй контроллер будет отслеживать положение шарика по оси Y и управлять вращением платформы вокруг оси X (Roll).

MiniPID pid_x;
MiniPID pid_y;

На вход контроллера подаём координаты шарика на соответствующей оси в миллиметрах. Цель контроллера — поддерживать шарик в центре экрана, то есть в точке с координатами (0, 0).

pid_x = new MiniPID(0.0009, 0.000, 0.0075);
pid_x.setSetpoint(0);
pid_y = new MiniPID(0.0009, 0.000, 0.0075);
pid_y.setSetpoint(0);

На выходе из контроллеров получаем необходимые нам векторы вращения платформы — R.y (Pitch) и R.x (Roll). Затем матрицу с новыми векторами отправляем на расчёт в класс platfrom.

R.y = (float) pid_x.getOutput(ball_x, 0);
R.x = (float) pid_y.getOutput(ball_y, 0);
platform.applyTranslationAndRotation(T, R);

По сути, теперь два ПИД-регулятора управляют двумя слайдерами нашего графического интерфейса приложения Processing.

В новой версии приложения мы изменили отображение платформы с эллипса на прямоугольник размером с наш сенсорный экран, а также визуализировали вектор текущего положения шарика на платформе.

Готово! Запускаем приложение и подбираем пропорциональный (P), интегрирующий (I) и дифференцирующий (D) коэффициенты для ПИД-регулятора, пока шарик не перестанет падать с платформы.

Вот что у нас получилось:

Точной настройкой ПИД-контроллеров в этом эксперименте мы не занимались и выбрали первые подходящие коэффициенты. Интегрирующая составляющая у нас и вовсе отсутствует.

Пара важных обнаруженных нюансов.

Наша база с сервоприводами получилась не очень устойчивой. Во время контроля сервоприводы могут совершать довольно резкие движения и по инерции двигать всю базу целиком. Поэтому базу лучше надёжно закрепить винтами или утяжелить. В качестве груза мы использовали три круглые куски фанеры толщиной 10 мм.

Обязательно постарайтесь выставить максимально горизонтальное положение платформы в изначальном виде. Платформу нужно выставить по уровню, например, используя мобильное приложение. Для корректировки можно поиграть с шириной ШИМ-импульса для сервоприводов в положении 0°. Или можно просто подложить что-нибудь под базу.

Платформа не будет катать шарик вечно. Рано или поздно шарик придёт в состояние баланса и остановится. Внимательно посмотрите, в какой именно точке платформы шарик поймал равновесие. Подстройте свою платформу так, чтобы эта точка была максимально близко к реальному центру платформы.

Платформа-балансир на Raspberry Pi

В том виде, в каком есть, платформу Стюарта решили поставить в магазине-шоуруме Амперки, чтобы каждый наш гость мог попинать шарик на платформе и оценить устройство в действии.

Чтобы не возиться с персональным компьютером, мы решили управлять платформой с микрокомпьютера Raspberry Pi 5.

Для более быстрой работы платформы-балансира мы портировали программу c языка Processing на Python. К слову, почти весь код для нас перевела нейросеть ChatGPT.

#!/usr/bin/python3

import numpy as np
import serial
from simple_pid import PID
import time

serial_port = '/dev/ttyUSB0'
baud_rate = 115200
serial_connection = serial.Serial(serial_port, baud_rate)

TOUCHSCREEN_WIDTH = 225.0
TOUCHSCREEN_HEIGHT = 171.5
ball_x = 0.0
ball_y = 0.0

BASE_ANGLES = np.array([-50.0, -70.0, -170.0, -190.0, -290.0, -310.0])
PLATFORM_ANGLES = np.array([-54.0, -66.0, -174.0, -186.0, -294.0, -306.0])
BETA = np.array([np.pi / 6, -5 * np.pi / 6, -np.pi / 2, np.pi / 2, 5 * np.pi / 6, -np.pi / 6])
BASE_RADIUS = 76.0
PLATFORM_RADIUS = 60.0
HORN_LENGTH = 40.0
ROD_LENGTH = 130.0
INITIAL_HEIGHT = 120.28183632
  
b = np.array([[0.0, 0.0, 0.0], [0.0, 0.0, 0.0], [0.0, 0.0, 0.0], [0.0, 0.0, 0.0], [0.0, 0.0, 0.0], [0.0, 0.0, 0.0]])
p = np.array([[0.0, 0.0, 0.0], [0.0, 0.0, 0.0], [0.0, 0.0, 0.0], [0.0, 0.0, 0.0], [0.0, 0.0, 0.0], [0.0, 0.0, 0.0]])
q = np.array([[0.0, 0.0, 0.0], [0.0, 0.0, 0.0], [0.0, 0.0, 0.0], [0.0, 0.0, 0.0], [0.0, 0.0, 0.0], [0.0, 0.0, 0.0]])
l = np.array([[0.0, 0.0, 0.0], [0.0, 0.0, 0.0], [0.0, 0.0, 0.0], [0.0, 0.0, 0.0], [0.0, 0.0, 0.0], [0.0, 0.0, 0.0]])
alpha = np.array([0.0, 0.0, 0.0, 0.0, 0.0, 0.0])
        
T = np.array([0.0, 0.0, 0.0])
R = np.array([0.0, 0.0, 0.0])
initial_height = np.array([0.0, 0.0, INITIAL_HEIGHT])

def initialize_platform():
    for i in range(6):
        xb = BASE_RADIUS * np.cos(np.radians(BASE_ANGLES[i]))
        yb = BASE_RADIUS * np.sin(np.radians(BASE_ANGLES[i]))
        b[i] = [xb, yb, 0]
        px = PLATFORM_RADIUS * np.cos(np.radians(PLATFORM_ANGLES[i]))
        py = PLATFORM_RADIUS * np.sin(np.radians(PLATFORM_ANGLES[i]))
        p[i] = [px, py, 0]

def calculate_angle_alpha():
    for i in range(6):
        q[i][0] = np.cos(R[2]) * np.cos(R[1]) * p[i][0] + (-np.sin(R[2]) * np.cos(R[0]) + np.cos(R[2]) * np.sin(R[1]) * np.sin(R[0])) * p[i][1] + (np.sin(R[2]) * np.sin(R[0]) + np.cos(R[2]) * np.sin(R[1]) * np.cos(R[0])) * p[i][2]
        q[i][1] = np.sin(R[2]) * np.cos(R[1]) * p[i][0] + (np.cos(R[2]) * np.cos(R[0]) + np.sin(R[2]) * np.sin(R[1]) * np.sin(R[0])) * p[i][1] + (-np.cos(R[2]) * np.sin(R[0]) + np.sin(R[2]) * np.sin(R[1]) * np.cos(R[0])) * p[i][2]
        q[i][2] = -np.sin(R[1]) * p[i][0] + np.cos(R[1]) * np.sin(R[0]) * p[i][1] + np.cos(R[1]) * np.cos(R[0]) * p[i][2]
        q[i] += T + initial_height
        l[i] = q[i] - b[i]
    for i in range(6):
        L = np.linalg.norm(l[i]) ** 2 - ((ROD_LENGTH ** 2) - (HORN_LENGTH ** 2))
        M = 2 * HORN_LENGTH * (q[i][2] - b[i][2])
        N = 2 * HORN_LENGTH * (np.cos(BETA[i]) * (q[i][0] - b[i][0]) + np.sin(BETA[i]) * (q[i][1] - b[i][1]))
        alpha[i] = np.arcsin(L / np.sqrt(M ** 2 + N ** 2)) - np.arctan2(N, M)
        if np.isnan(alpha[i]):
            alpha[i] = 0
             
def send_angles_to_serial(alpha):
    data = 'j' + 'j' + ','.join([str(int(np.degrees(alpha_i) * 100)) for alpha_i in alpha]) + '\n'
    serial_connection.write(data.encode())
    
def read_serial_event():
    if serial_connection.in_waiting >= 6:
        header = serial_connection.read(2)
        if header == b'kk':
            global ball_x, ball_y
            ball_x = int.from_bytes(serial_connection.read(2), byteorder='little', signed=True)
            ball_y = int.from_bytes(serial_connection.read(2), byteorder='little', signed=True)
            
if __name__ == "__main__":   
    initialize_platform()
    
    pid_x = PID(0.001, 0.000, 0.00042, setpoint=0, output_limits=(-0.6, 0.6))
    pid_y = PID(0.001, 0.000, 0.00042, setpoint=0, output_limits=(-0.6, 0.6))
    
    last_time = time.time()
    
    while True:
        read_serial_event()
        
        current_time = time.time()
        elapsed = current_time - last_time
        
        if elapsed >= 0.02:
            T = [0, 0, 0]
            R = [pid_y(ball_y), pid_x(ball_x), 0]
    
            calculate_angle_alpha()
            send_angles_to_serial(alpha)
        
            print("ball: ", ball_x, " ",ball_y, " alpha: ", np.degrees(alpha))        
            last_time = current_time

Для линейной алгебры мы использовали библиотеку NumPy, а для ПИД-контроллера — библиотеку simple-pid.

Заключение

Платформа Стюарта — это крайне интересный и познавательный проект! Доведя этот эксперимент до ума, можно использовать его, например, в качестве курсовой работы в техническом вузе.

Эксперимент с катанием шарика кажется немного «притянутым за уши», ведь мы не полностью используем все степени свободы платформы. Но зато у нас получился отличный задел под будущие эксперименты. В следующий раз мы попробуем заставить платформу Стюарта бесконечно чеканить теннисный мячик!